Contents
The content of this page is as below:
- Recap - Vapour-Liquid Equilibria
- Short-Cut Distillation Design
- Operation of Distillation Columns
- Distillation Column Sequencing
- Short-Cut Design for Complex Columns
- Recap - Non-Ideal Vapour-Liquid Equilibria
- Feasible Distillation Regions
- Short-Cut Design for Azeotropes
- Distillation Sequences for Azeotropes
The slides for all the recordings below can be downloaded as the
| Slide Pack of recap folder |
Recap - Vapour-Liquid Equilibria
You should remember from previous study that the status of a matter existing in our physical world is determined by pressure and temperature. At the right temperature and pressure, a matter can be solid, liquid or vapour. In thermodynamics, the three phases can coexist - interpreted as phase equilibrium at a particular point of temperature and pressure. In distillation, we are normally concerned with the vapour-liquid equilibrium in multi-component mixtures. The video below gives you a quick reminder of this vapour-liquid equlibria in case you can't remember this:
Short-Cut Distillation Design
It is possible to design multi-component distillation using some short-cut equations, the basic assumptions for these include,
- constant relative volatility, which is the most important assumption for most problems although not often a good assumption for mixtures with non-ideal behaviour, and
- constant molar overflow i.e. constant molar vapour and liquid flowrates on each stage of the distillation column.
The video below discusses these short-cut equations:
The full derivations of the short-cut equations can be downloaded from the following document:
| Derivations |
Example
Use the short-cut method to design a distillation column to separate the mixture in the table below, with a recovery of 95% of C5 to the distillate and 97% of C6 to the bottom product. Use a saturated liquid feed at 298K with a column pressure equal to the feed pressure.
| Alkane | mol fraction |
| C3 | 0.05 |
| C4 | 0.10 |
| C5 | 0.40 |
| C6 | 0.35 |
| C7 | 0.10 |
The saturation pressure in kPa for any straight chained hydrocarbon length n at a temperature in K can be approximated to,
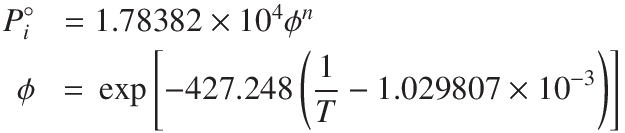
| Answer |
The video below shows how you can impliment these methods in HYSYS:
Operation of Distillation Columns
There are some general considerations in designing a multi-component distillation. As many components are present in the feed, fixing the recovery or mole fraction of a single component does not specify the product composition or temperature; also, the selection of the key components is a process engineering decision, usually based on the objectives of the separation. Mass and energy balances are solved iteratively. It is useful to use commercial process simulation software to carry out the calculations. The short-cut design equations allow initial estimates of design variables and column performance to be obtained prior to rigorous simulation. Practical experience shows that convergence of rigorous simulation can be facilitated by good initial estimates. The video below discusses some of the key operating parameters that we need to consider when desiging our distillation columns:
Some quantitative performance indicators are proposed for screening distillation sequences as discussed in the video above. Some useful information for these can be seen in the document below:
Distillation Column Sequencing
In almost any chemical industry, the mixtures intended to be separated are not simple binary mixtures, they normally contain more than two components. If the mixture is homogeneous, i.e. a single phase, distillation would be the most commonly used method for separating those multiple components. However, if the products required are not only two but more than that, then generally a separation sequence is needed to make the separation of the components in a viable and economic way. This is called distillation sequencing; the separations carried out based on distillation does not have only one sequence but other alternatives. The problem then becomes how to sieve those sequences and choose the best option. The video below discusses this concept and provides some heuristic rules:
In addition to simple distillation columns, complex distillation columns can be considered. These can have more than 2 product streams, or have linking between columns by two-directional flows with one column having no condenser, or no reboiler - often referred to as thermally coupled distillation columns. In sequencing distillation with complex columns, heuristics for simple columns are still available and useful as they provide qualitative guidance with insights; however, extra heuristics for the complex columns are also available. The video below discuses these:
Energy savings for using these systems can be examined for a three component system (A,B,C) based on the assumption of ideal separations. The energy use of the complex configuration can be compared to the energy use for the direct or indirect equivalent sequence, the section marked D is where the energy use of the direct sequence is less, and the section marked I is where the energy use of the indirect sequence is less. The graphs below show the percent saving (based on vapour flow rate) for using the complex configuration, and line to represent the relevant heuristics for comparison.
Is this web app not displaying correctly? Try opening it in a new window
The distillation sequencing heuristics can be sumarised as below:
| Download as a pdf Cheat Sheet |
Short-Cut Design for Complex Columns
When it comes to mass and energy balance analysis, it is practically useful to decompose complex columns into multiple columns so that short-cut calculations can be carried out relatively easily. Thermally coupled columns can be decomposed into a combination of side stream columns and simple columns. The mass and energy balances are equivalent for the complex column configurations and the decomposed multi-column sequence.
However, the capital costs would then depend on the actual configurations used. Generally speaking, the cost of complex column configuration is less than that of the equivalent sequence of columns. The video below discusses how this can be acheived:
Example
The mixture of A, B, C and D shown in the table below is to be separated into pure component products using a sequence of distillation columns. From the heuristics it has been identified that a potential sequence could be A/B/CD (pre-fractionator) -> C/D.
| Component | Molar composition | Relative volatility between adjacent components | Boiling point / oC | Liquid density / kg m-3 | Molecular weight / Da |
| A | 0.20 | 2.33 | 36 | 0.5 | 72 |
| B | 0.50 | 2.33 | 68 | 0.6 | 86 |
| C | 0.25 | 1.148 | 98 | 0.7 | 100 |
| D | 0.05 | - | 151 | 0.8 | 128 |
Design the columns required if the feed flow rate is 300 kmol hr-1. Assume a 99% split of the key components in each relevant section and an R/Rmin =1.
| Answer |
Recap - Non-Ideal Vapour-Liquid Equilibria
You should be able to remember from previous courses that departures from Raoult’s law commonly manifest themselves in the formation of azeotropes. Many close boiling, non-ideal mixtures form azeotropes, particularly those of different chemical types. The video below provides a quick reminder of this topic:
The graph below shows the x-y diagram (left) and the T-x-y diagram (right) for a non-ideal system with differences in the solubility parameter, δ. This is the prediction from regular solution theory; although this is very useful, as only the pure component solubility parameters are needed (as opposed to experimentally fitted values for the mixture), it lacks in the fact that it always predicts activity coefficients higher than unity. This means that the properties for mixtures can only be predicted if they are non-ideal in the fact that when they mix they have positive excess free energy of mixing (i.e. they dislike mixing with each other).
Is this web app not displaying correctly? Try opening it in a new window
Feasible Distillation Regions
In the distillation of a ternary mixture, possible equilibrium compositions do not lie uniquely on a single, isobaric equilibrium curve because the Gibbs phase rule gives an additional degree of freedom. The other compositions are determined only if the temperature, pressure, and composition of one component in one phase are fixed.
Therefore, the feasible-distillation regions for azeotrope-forming ternary mixtures are not obvious. Fortunately, residue-curve maps can be used to make preliminary estimates of regions of feasible-product compositions for non-ideal ternary systems. These regions are determined by superimposing a column material-balance line on either type of curve-map diagram. The video below introduces ternary diagrams for distillation, how to produce residue curves, and how to use these residue curves to calculate feasible separations:
The figure below shows an example of an actual distillation column with a finite reflux ratio (R = 1) plotted on a residue curve plot for Hexane, Octane, and Decane. The rectifying section (red dots) approximately follows the residue curve that D is on. The stripping section (blue dots) also follows the same residue curve from the other direction, starting at B. There is some deviation around the feed point (stage 11), due to the fact that the feed addition affects the equilibrium in column. The green line is the approx mass balance between the feed (green dot), and the trays in the rectifying and stripping sections.
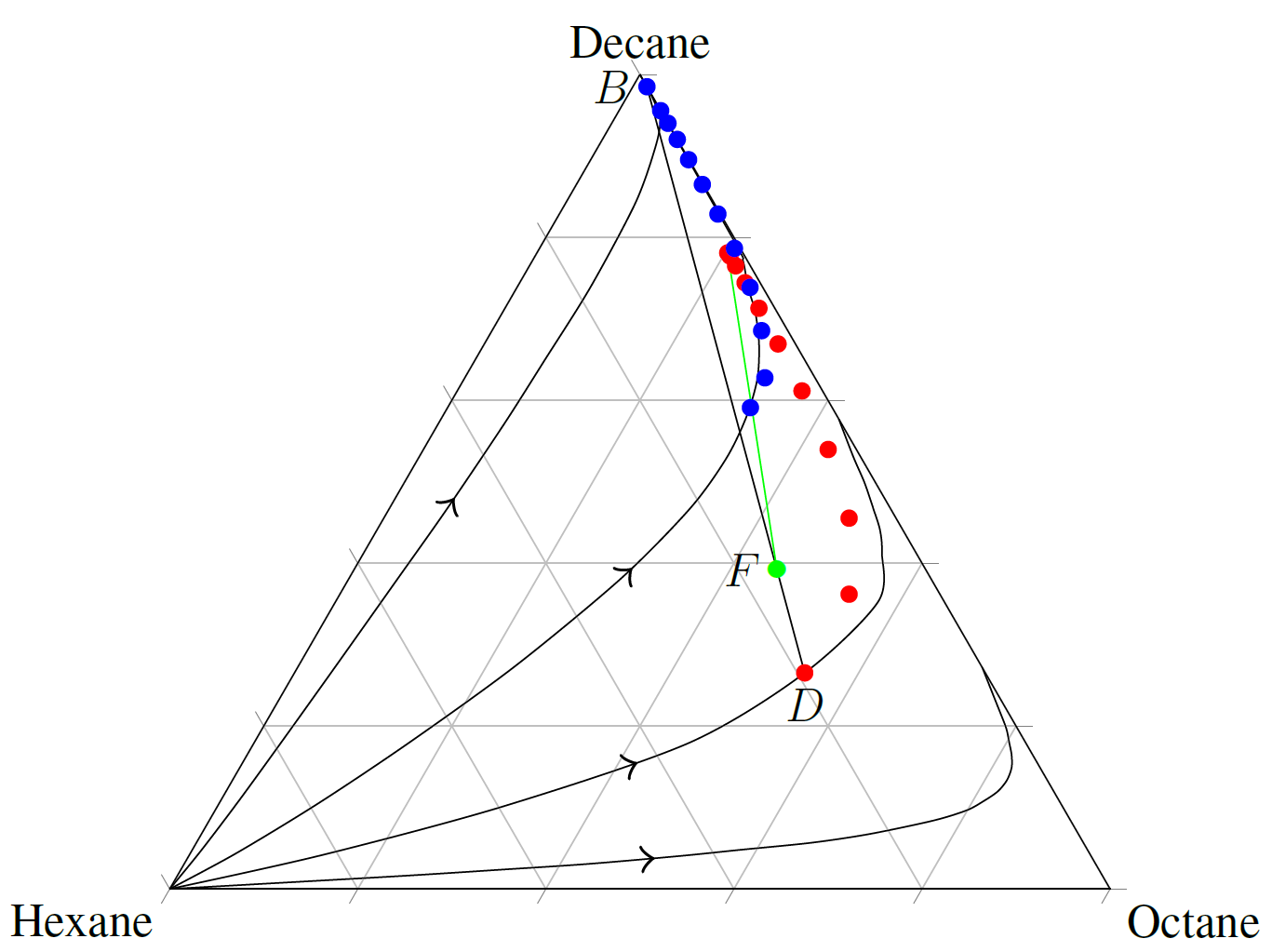
Example
Plot a portion of a residue curve for n-propanol (1), isopropanol (2), and benzene (3) at 1 atm starting from a bubble-point liquid with 20 mol% each of 1 and 2, and 60 mol% of component 3 (78.67 oC). Use Raoult's law with regular-solution theory for estimating the liquid-phase activity coefficients. The normal boiling points of the three components in oC are 97.3, 82.3, and 80.1 respectively. Minimum-boiling azeotropes are formed at 77.1 oC for components 1, 3 and at 71.7 oC for 2, 3.
Useful information:
R = 1.987 cal mol-1 K-1
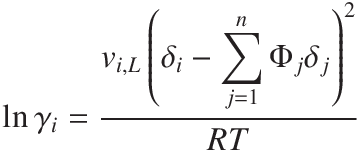 |
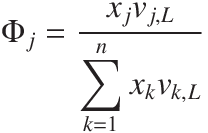 |
| Component | δ / cal1/2 cm-3/2 | v / cm3 mol-1 | A | B | C |
| n-propanol | 12.0 | 74.72 | 16.1154 | 3483.67 | 205.807 |
| isopropanol | 11.6 | 76.40 | 16.6796 | 3640.20 | 219.610 |
| benzene | 9.2 | 89.04 | 13.7819 | 2726.81 | 217.572 |
The temperature of the system can be calculated from,
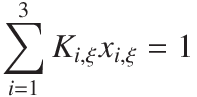
The vapour concentration in equlibrium with the liquid phase can then be calculated from,
![]()
The next step liquid composition can then by calculated from the forward-finite-difference form of the residue curve equation,
![]()
Instead of calculating all three componets, it is better numerically to calculate two and then the third from a balance of the liquid phase,
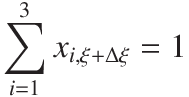
| Answer |
The video below shows how these can be calculated with Aspen Properties:
Short-Cut Design for Azeotropes
Previously, the short-cut method was discussed for multi-component distillation. One of the key assumptions for this method is a constant relative volatility (or approximately constant). When a system has an azeotrope it is clear that the relative volatility is not constant. The video below discusses a method to allow the short-cut methods to be used with azeotropic systems:
Example
A distillation column is used to seperate the the feed shown in the table below into the specified distillate and bottoms products. It is discovered that this system actually contains an azeotrope between Methanol and Methyl acetate that forms a distillation boundary with the pure Ethanol. The azeotrope has a composition of 65.74% Methyle acetate and 34.26% Methanol and has the lowest boiling point in the system.
| Component | Feed | Bottoms | Distillate | |||
| xi | α | xi | α | xi | α | |
| Methyle Acetate | 0.200 | 4.436 | 0.020 | 5.487 | 0.630 | 3.024 |
| Methanol | 0.600 | 1.973 | 0.705 | 1.772 | 0.350 | 2.905 |
| Ethanol | 0.200 | 1.000 | 0.275 | 1.000 | 0.020 | 1.000 |
If the short-cut equations are to be used to design this system, what should be the 3 pseudo-components used, the adjusted compositions of the inlet and outlet flows, and the average relative volatility for each component?
| Answer |
Distillation Sequences for Azeotropes
When α < 1.10, separation by ordinary distillation may be uneconomical, and even impossible if an azeotrope forms. The video below discusses some special distillation sequences that can be used in this case:
Heterogeneous azeotropic distillation can be used to separate close-boiling binaries and minimum-boiling binary azeotropes by employing an entrainer that forms a binary and/or ternary heterogeneous (two-phase) azeotrope. A heterogeneous azeotrope has two or more liquid phases. If it has two, the overall, two liquid-phase composition is equal to that of the vapour phase. Thus, all three phases have different compositions. The sequence below provides an example two column system. The ternary diagram below shows the position of the columns and the relevant separations formed to produce output of pure A and B from the initial feed of a mixture of A and B.
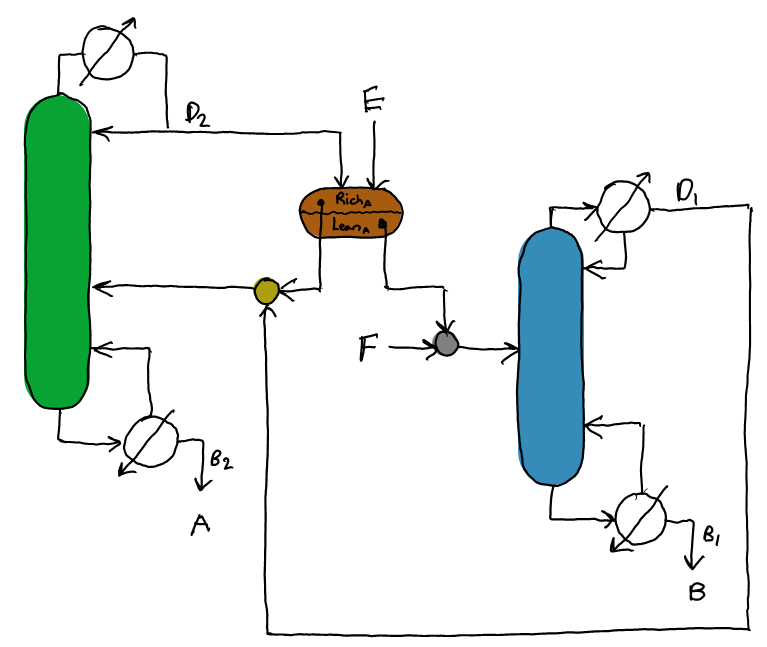
Is this web app not displaying correctly? Try opening it in a new window
The video below provides an example of setting up an Azeotropic distillation system in HYSYS: