Contents
This week we are covering Mass Transfer effects on catalytic reactions. Material in this week covers course ILOs 1 and 3 and may be in the Mid Session Exam. This content will not be in the final exam.
The content for this week is below:
- 1. ILOs
- 2. Introduction
- 3. External Mass Transfer
- 4. Effect of External Mass Transfer on Surface Reaction Rate
- 5. Internal Mass Transfer
- 6. Reaction Effectiveness Factor
- 7. Global Reaction Rate
The slides for all the recordings for this week can be downloaded in the weekly slide pack.
1. ILOs
After completion of this weeks material you should be able to:
- Develop expressions for concentration profile of species undergoing external mass transfer through a boundary layer.
- Calculate the reaction rate for an external mass transfer limited non-porous catalyst particle.
- Develop expressions for concentration profile of species undergoing various reactions in a porous catalyst pellet.
- Calculate the Thiele modulus and effectiveness factor to determine the rate limiting step: pore diffusion versus reaction.
- Derive an expression for the overall rate of a catalytic reaction with both external mass transfer and internal pore diffusion
2. Introduction
Over the last couple of weeks you should have become familiar with the seven steps in heterogeneous catalytic reactions,

You have already examined in detail how steps 3 and 5 effect the rate of reaction (step 4). Now we are going to focus on the effects of steps 1, 2, 6, and 7 on the rate of the reaction. These steps can be divided into two key areas,
- External Diffusion (Steps 1 and 7)
- Internal Diffusion (Steps 2 and 6)
3. External Mass Transfer
The external mass transfer is determined by the boundary layer around the object. The video below reviews the derivation of a molar balance through a unit zone and then shows how we can use this to calculate the mass transfer rate across the boundary layer:
From the video it is clear that the key parameter for the mass transfer is the mass transfer coefficient, kc, in m s−1. This is dependent on the diffusion coefficient and the boundary layer thickness, and thus is complex to calculate. This means that typically correlations have been created for different situations to allow us to find values of the mass transfer coefficient. Some examples of these are given below, which use some key dimensionless numbers,

where ε is the bed porosity.
4. Effect of External Mass Transfer on Surface Reaction Rate
Now that we have an expression for the mass transfer through the boundary layer, we can examine its affect on the overall reaction rate. The video below derives the overall reaction rate for a non-porous catalyst particle with a fist order surface reaction:
The oveall reaction rate is dependant on the surface reaction rate constant and the mass transfer constant. The graph below gives an example of the variation of the total surface reaction rate with the superficial fluid velocity for a packed bed of spherical particles. The reaction rate constant and the particle diameter can be varied using the sliders. At low velocity the total reaction rate is controlled by the rate of the mass transfer while at high velocity it is controlled by the rate of the reaction.
Is this web app not displaying correctly? Try opening it in a new window
Using the same mathods as in the video above it is possible to derive the rate equation for a general order surface reation, in this case we do not get an explicit expression,
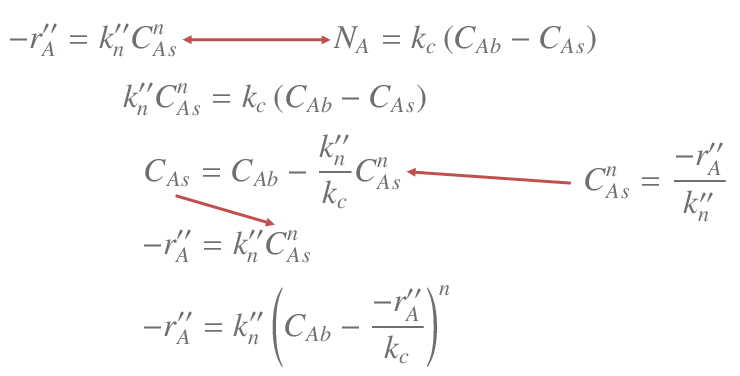
5. Internal Mass Transfer
We have just looked at the effect of extermal mass transfer on the global reaction rate of a non-porous catalyst particle. If the catalyst particle is porous then the reactant will move into the particle as it reacts as thus the internal mass transfer is important. The video below reviews a mole balance in spherical coordinates and then shows how this can be used to calculate the concentration profile though the particle.
The concentration profile inside the particle is dependant on the dimensionless parameter Φ. The parameter is known as the Thiele Modulus. The full derivation of the concentration profile can be seen in this document (please note you will not be tested on this derivation, it is just for interest).
Ernest W. Thiele

The graph below gives an example of the concentration profile through the catalyst particle at different values of the thiele modulus, which can be varied with the slider. The right hand side of the graph is the outside of the particle and the left hand side is the centre of the particle. At low values of the Thiele modulus the surface reaction is rate limiting and thus the concentrion in the pores is equal to that at the outside of the particle. At high values of the Thiele modulus the internal diffusion is rate limiting and thus the concentration in the pores quickly drops to almost nothing.
Is this web app not displaying correctly? Try opening it in a new window
The Thiele modulus used above is for a first order reaction; however, a general Thiele modulus can be defined for a general reaction order, n, using the same method as in the video above, this gives,
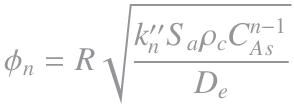
6. Reaction Effectiveness Factor
As the concentration through the particle varies, the reaction rate varies with position in the particle. This means that it makes sence to define an effectiveness, which allows comparision to a single known reaction rate. The video below derives the effectiveness factor for a spherical particle with a first order reaction:
The derivation in the video can also be carried out for other shapes of particles. The derivations for these are complex and thus the results are just given below for 1st order reactions (note the slight difference in the Thiele module used here),
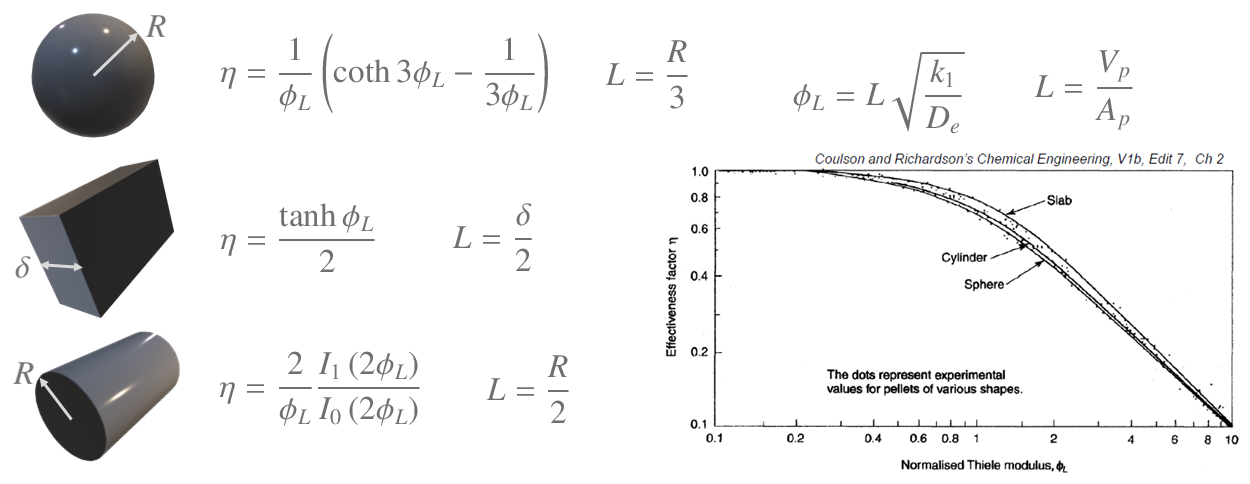
I1 and I0 are Bessel functions.
The same process can also be carried out for different orders of reactions for spherical particles. The form of the general expression for the effectiveness is very complex, but the approximation for large values of the Thiele modulus (i.e. where there is need to take into account the mass transfer limitation) is quite simple as below,
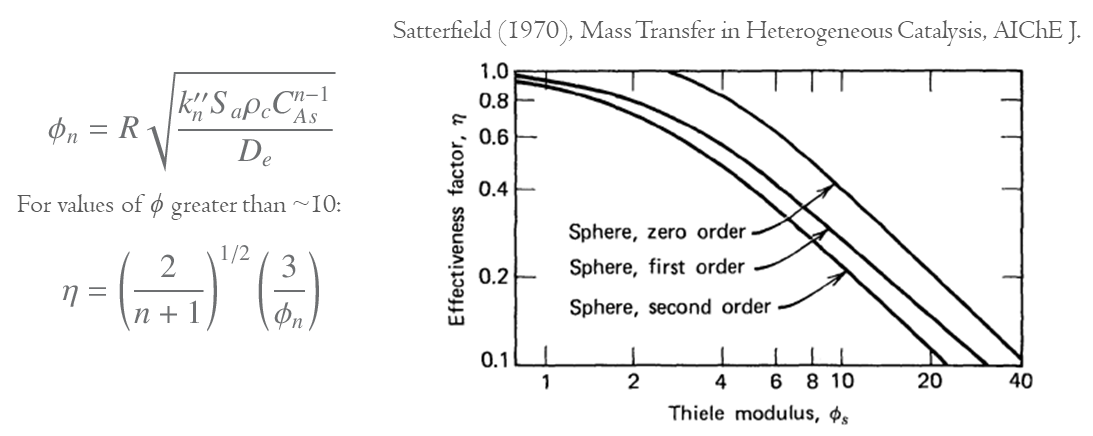
7. Global Reaction Rate
In the topics above we have looked at external mass transfer and internal mass transfer, but seperately. In many systems we have porous catalysis but some external mass transfer effects. The video below examines the global reaction rate where the rate of reaction is taken from the bulk concentration with both external and internal mass transfer effects,
Amadeo (1995) examine the reaction rate of the low-temperature water-gas sift reaction. To do this they use a small amount of a powdered catalyst and product a full reaction model with surface adsorption kinetics as,
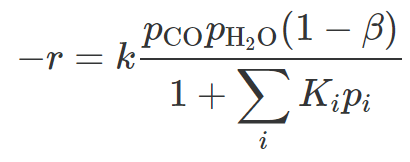
where
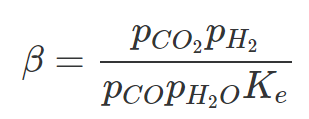
Which is for the equlibrium of the reaction.
This provides a good model for the reaction rate. However, it does not take into account the effects of using real catalyst pellets with mass transfer. This can be taken into account by using the Overall Effectiveness Factor, Ω
Moe (1963) examine the reaction rate on an industrial system with an approximately 2 cm diameter catalyst. The equation they produced is not from first principles, but just empirically correlates the data.
The graph below shows the variation of the reaction rate with catalyst size. The limitation is the internal mass transfer in the pores as the external mass transfer rate is higher than the reaction rate.
Is this web app not displaying correctly? Try opening it in a new window
Now that we have expressions for the rate of reactions with mass transfer effects we can design catalytic reactors by inserting these rates into the key design equations. The video below gives a simple integratable example for a single first order reaction,
References:
N. E. Amadeo and M. A. Laborde (1995), "Hydrogen Production from the Low-Temperature Water-Gas Shift Reaction: Kinetics and Simulation of the Industrial Reactor", International Journal of Hydrogen Energy, 20:949-965.
J. M. Moe (1963), "Low-temperature CO conversion", Symposium on Production of Hydrogen, Am. Chem. Sot. Div. Petr. Chem. B29.